It is likely one of the most crucial subjects at any time when. It’s associated to the resistance a fluid faces in movement. A fluid exerts a drive on a physique in a distinct course. Now the primary query is, what’s drag? And what can we learn about it?
What’s Drag?
The definition of drag is as follows:
The drive exerted on a flowing fluid within the course of fluid move is named drag.
A number of the important key factors associated to the drag are as follows:
In an effort to elaborate on the drag drive by way of an instance. The physique is hooked up to calibrated spring, and it’s used to measure the displacement within the course of move.
The drag balances are a type of units which are generally used to measure the drag drive.
It’s not incorrect to say that the drag drive is way much like the frictional drive.
The extra discount within the drag drive, the much less gasoline will likely be consumed.
An attention-grabbing reality about drag is that we are able to additionally produce a helpful impact by drag, so we have to maximize its worth. On this state of affairs, drag helps in pollen flying, utilization of parachutes, motion of leaves and way more. These are one of many frequent examples utilized in our every day life.
The drag drive is a mixture of strain and the wall shear forces within the move course.
What’s Raise?
In an effort to clarify the elevate in simple phrases, allow us to take a look on the definition.
The part of strain and the wall shear forces within the regular course to the fluid move that tends to maneuver the physique in that course is named elevate.
A number of the necessary key factors associated to the elevate is as follows:
Each time we’re coping with elevate and drag, these each have completely different tasks. Within the case of two-dimensional move, the resultant of the shear and the strain forces are divided into two necessary elements. The move in a single course solely is the drag drive, whereas the conventional move is the elevate.
Mathematical Presentation of Raise and Drag:
The elevate and drag have the equations by way of we are able to discover the correct values theatrically and might examine them with the sensible ones.
dFD=-P dAcos +wdAsin
dFL=-P dAsin -wdAcos
FD=∫AdFD=∫A(-Pcos +wsin )dA
FL=∫AdFL=-∫A(Psin +wcos )dA
The above equations present the pores and skin friction (wall shear) and strain, which contribute to the drag and elevate.
The elevate and the drag are a robust operate of angle assault.
The drag and elevate forces depend upon the upstream velocity, density, dimension, form, and orientation of the physique. It’s higher to work with the dimensionless numbers which are used for the illustration of drag and elevate traits of the physique.
The drag and elevate coefficient equations are as follows:
CD=FD12V2A
CL=FL12V2A
Right here A is the ordinarily Frontal Space.
Friction and Stress Drive
The subject is said to tug and elevate. In an effort to outline the friction and strain forces, I’ll clarify in few key factors:
Pores and skin Friction Drag:
The a part of due on to wall shear stress referred to as pores and skin friction drag.
Stress Drag
It’s the half that’s due on to the strain P, referred to as the strain drag.
CD, friction=FD, friction12V2A
CD,strain=FD,pressure12V2A
So these are the drag coefficients of strain and friction.
If the values of those coefficients can be found, then it turns into simpler for us to seek out the worth of the full drag coefficient and whole drag drive. The formulae of each of those are given as follows:
CD=CD,friction+CD,strain
FD=FD,friction+FD,strain
The friction of drag is the primary part of the wall shear drive, and this drive is within the course of move.
Within the case of a flat floor, the worth of friction drag is zero, and it’s regular to the move course. The worth is alleged to be the utmost for a flat floor parallel to the move.
With the rise within the viscosity, there is a rise within the drag.
One other thrilling reality about it’s that Reynold’s Quantity is inversely proportional to the viscosity of a fluid. So when the worth of Reynold’s quantity is excessive, then the worth of the full drag or the friction drag is much less.
When the worth of Reynold’s quantity is much less, it’s as a result of friction drag and largely occurs within the streamlined our bodies.
the our bodies having a big floor space have a major friction drag worth. However it’s impartial of the floor roughness.
Within the case of strain drag, it’s proportional to the frontal space.
The worth of drag strain for the blunt our bodies is most; for the streamlined our bodies is much less, and within the case of the skinny flat plates which are parallel to the move, the worth is zero.
Decreasing Drag by Streamlining
Additionally it is one of many necessary subjects of drag.
The next are some necessary key factors associated to decreasing drag by streamlining:
As I’ve mentioned earlier that the drag strain within the case of streamlined our bodies is much less.
Lower the drag for a streamlined physique by decreasing the move separation, finally decreasing the strain drag.
The streamlining delay the boundary layer separation leading to a lower within the strain drag and a rise in friction drag.
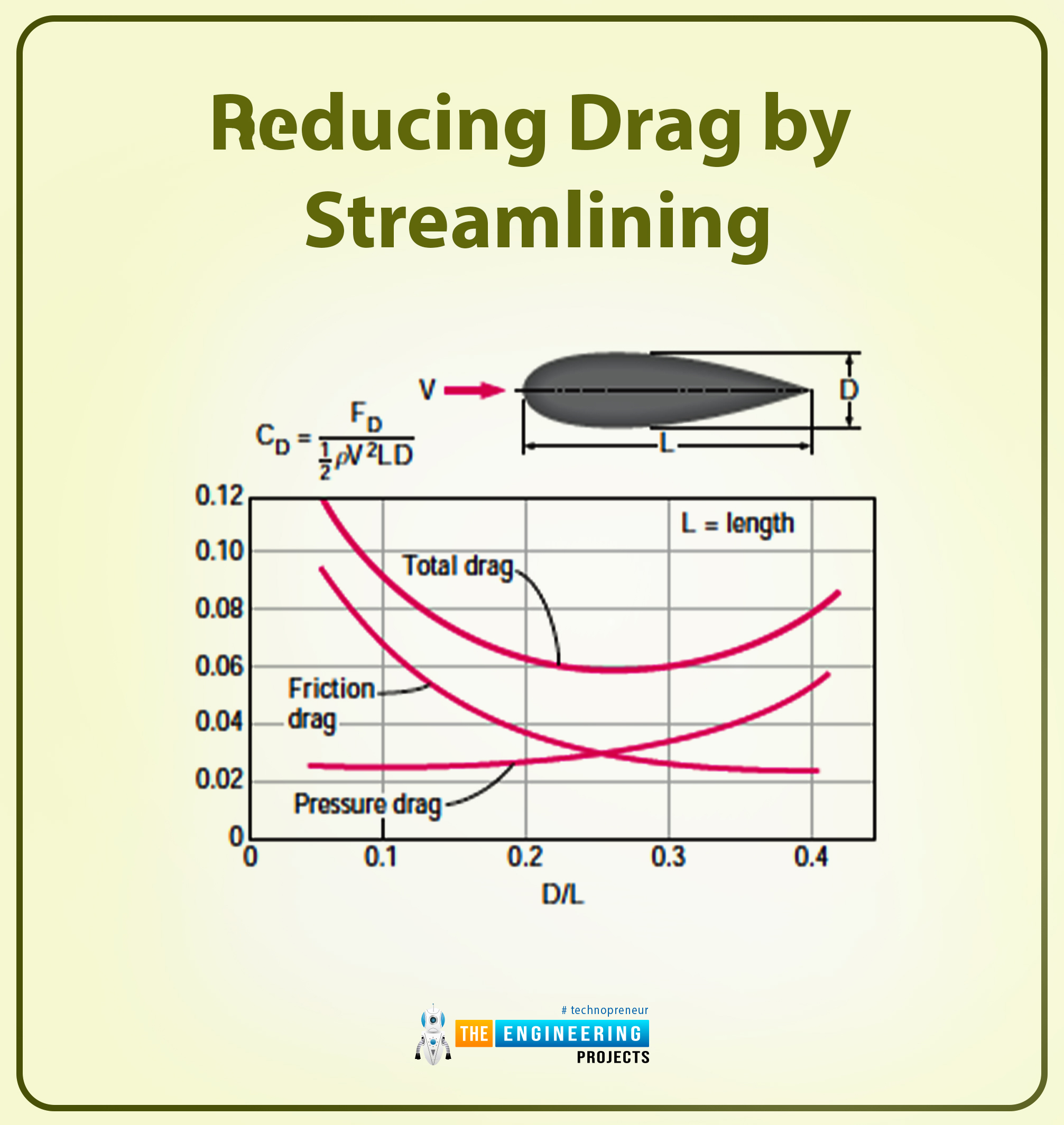
The next diagram reveals the distinction within the values of friction, strain, and whole drag coefficients of a streamlined strut.
As you possibly can see from the diagram, the worth of whole drag at minimal is D/L=0.25.
The drag coefficient worth will likely be 5 occasions within the case of a round cylinder having the identical thickness because the streamlined form.
Within the case of an elliptical cylinder form, the worth of the drag coefficient is much less. The elliptical cylinder form is taken into account the right instance for outlining the impact of streamlining on a drag coefficient.
Stream Separation
I’ll outline move separation extensively, so the next is the definition of it.
The fluid has excessive velocity when drive flows over a curved physique. Equally, fluid can climb uphill on a curved floor with out distraction.
At excessive velocities, the fluid stream detaches itself from the physique’s floor, often known as move separation.
A move might be separated from a floor when absolutely submerged in an immersed gasoline or liquid.
Parallel Stream over Flat Floor
There are numerous important terminologies for this subject, and the next are some necessary key factors, equations, and definitions for the parallel move over the flat floor. So allow us to begin.
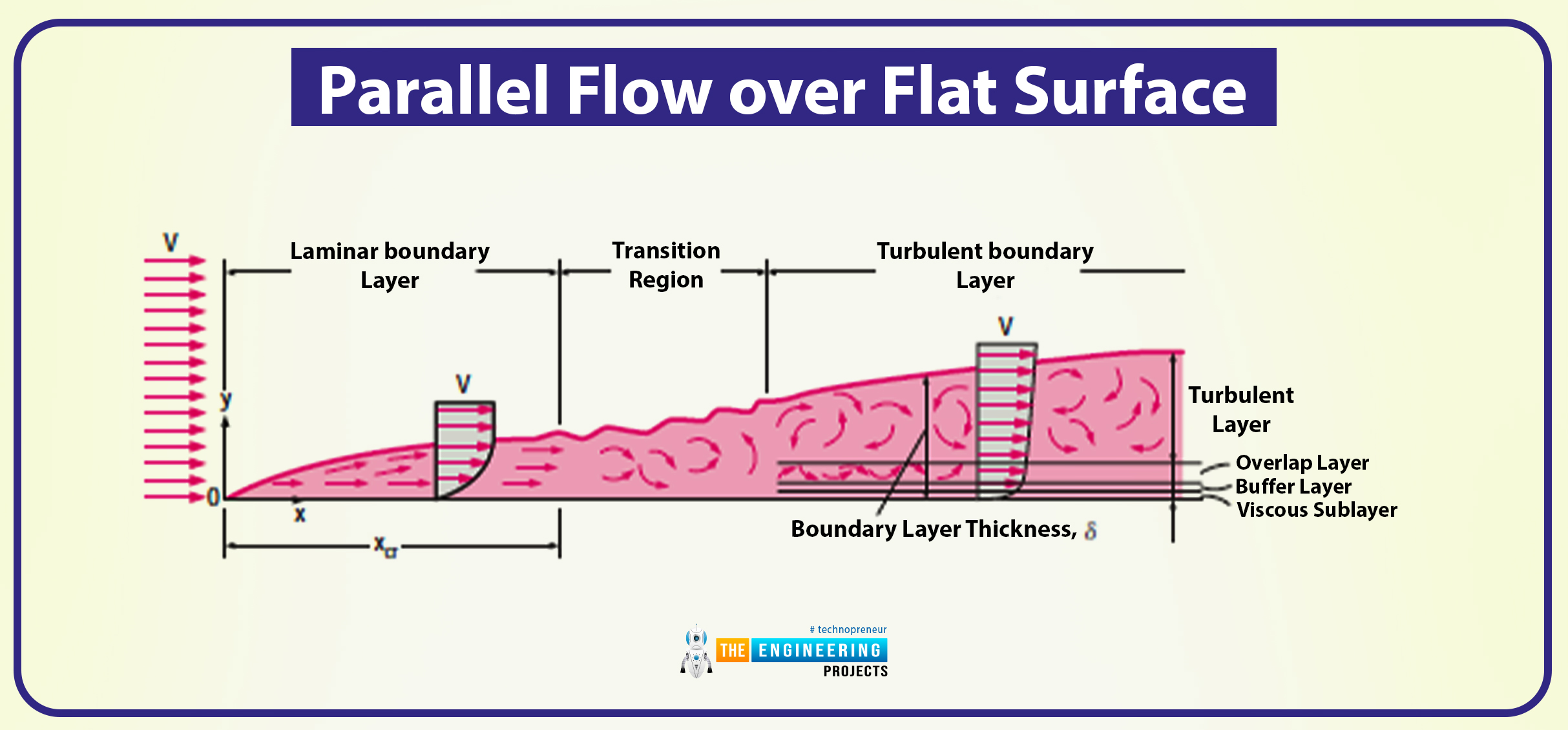
Taking this diagram as a reference, I’ll clarify the entire subject by way of this.
Right here, on this flat plate, the x-axis is measured alongside the plate floor (ranging from the forefront of the plate within the course the fluid is flowing), whereas the y-coordinate is measured from the floor within the regular course.
The floor’s velocity is the same as the speed of the fluid that travels alongside the x-coordinate.
As you possibly can see by way of the diagram, for our comfort, we now have assumed that the fluid is in adjoining layers and they’re piled onto each other
By doing so, the speed of the primary layer of fluid adjoining to the plate turns into zero, and that is as a result of no-slip situation.
The primary layer impacts the opposite layers by slowing the movement of particles of different completely different. And the method goes on because the layer slows down the subsequent layer’s molecules.
The presence of the layer is then felt as much as some regular distance (), from the plate, past which the free-stream velocity stays unchanged.
There are some vital areas and layers current on this layer, and they’re outlined as follows:
It’s the area of the move that’s above the plate bounded by regular distance () through which the impact of the viscous shearing drive attributable to fluid viscosity is felt.
It’s the area the place the frictional impact is negligible, and the speed is fixed.
The thickness of the boundary layer (δ) is the space y from the floor at which u=0.99V.
There’s a hypothetical line that’s current on the layer (u=0.99V) that divides the move into two areas, and they’re named as follows:
Boundary Layer Area
Irrotational Stream Area
On this flat plate parallel to the move situation, the strain drag is zero, and the drag coefficient equals the friction drag coefficient. Mathematically we are able to current it as follows:
CD=CD,friction=Cf
Right here Cf is the drag friction coefficient.
FD=Ff=12CfAρV2
Right here the A is the floor space of the plate.
From the diagram, you will have noticed that the speed profile is in laminar and turbulent flows.
Additionally, the turbulent is way fuller than the laminar one. Because it has 4 areas, and they’re named as follows:
Viscous Sublayer
Buffer Layer
Overlap Layer
Turbulent Layer
The transition of laminar to turbulent move relies on the geometry of the floor, roughness, upstream velocity, floor temperature, and plenty of issues.
The Reynold’s quantity at a distance x from the forefront of a flat plate is as follows:
Rex=ρVx=Vxv
Within the case of a flat easy plate, the transition from a laminar to a turbulent move begins at Reynold’s quantity RE≅1×105. The move doesn’t develop into turbulent till the worth of Reynold’s quantity reaches RE≅3×106
Friction Coefficient
The next are some key factors associated to the friction coefficients:
Within the case of laminar move, we are able to calculate the worth of friction coefficients through the use of the legislation of conservation of mass and momentum.
Within the case of turbulent move, it ought to be calculated experimentally and ought to be expressed within the empirical correlation.
The drag drive for the entire floor might be calculated through the use of the common friction coefficient worth.
In some circumstances, if we would like drag drive for a particular location, then on this situation, we should know the native worth of the friction coefficient.
If we now have the worth of native values, then it turns into simple for us to calculate the common friction coefficient values:
Cf=1L0LCf,xdx
Stream over Cylinders and Spheres
It is likely one of the necessary associated to elevate and drag. So following are the necessary key factors associated to the move over the cylinder and spheres:
In our every day life, if we glance round, there are a number of examples of it. In tubes (shell and tube warmth exchanger) entails the inner and exterior move over the tubes.
In sports activities, cricket, soccer, and tennis balls are one of the best examples of this subject.
For calculating the round cylinder or sphere, the exterior diameter is taken as D.
In Reynold’s quantity, the system is as follows:
Re=VDv
Right here the V stands for the uniform velocity of the fluid because it approaches the cylinder and sphere.
Right here, the worth of the vital Reynold’s quantity is Recr≅2×105.
The change in whole drag coefficient worth is noticed for the move of cylinders and spheres.
It’s not incorrect to say that the drag drive is as a result of friction drag on the low worth of Reynold’s quantity (Re< 10) and within the case of strain drag at a better worth of Reynold’s quantity (Re>5000).
The next diagram reveals the separation of the laminar boundary layer with the turbulent over a cylinder.
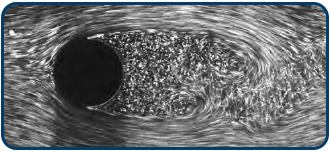
Impact of Floor Roughness
Within the earlier subject, I mentioned this factor that the influence of getting a floor makes an enormous distinction. So whereas discussing the cylinders and the spheres, it turns into necessary to debate them intimately.
The next are some important key factors associated to the subject:
The rise in floor roughness will increase the drag coefficient within the case of turbulent move.
For the streamlined case, it is usually the identical. However for the spheres and the cylinders, the rise within the roughness of the floor decreases the coefficient of drag. This implies they’ve an oblique relationship.
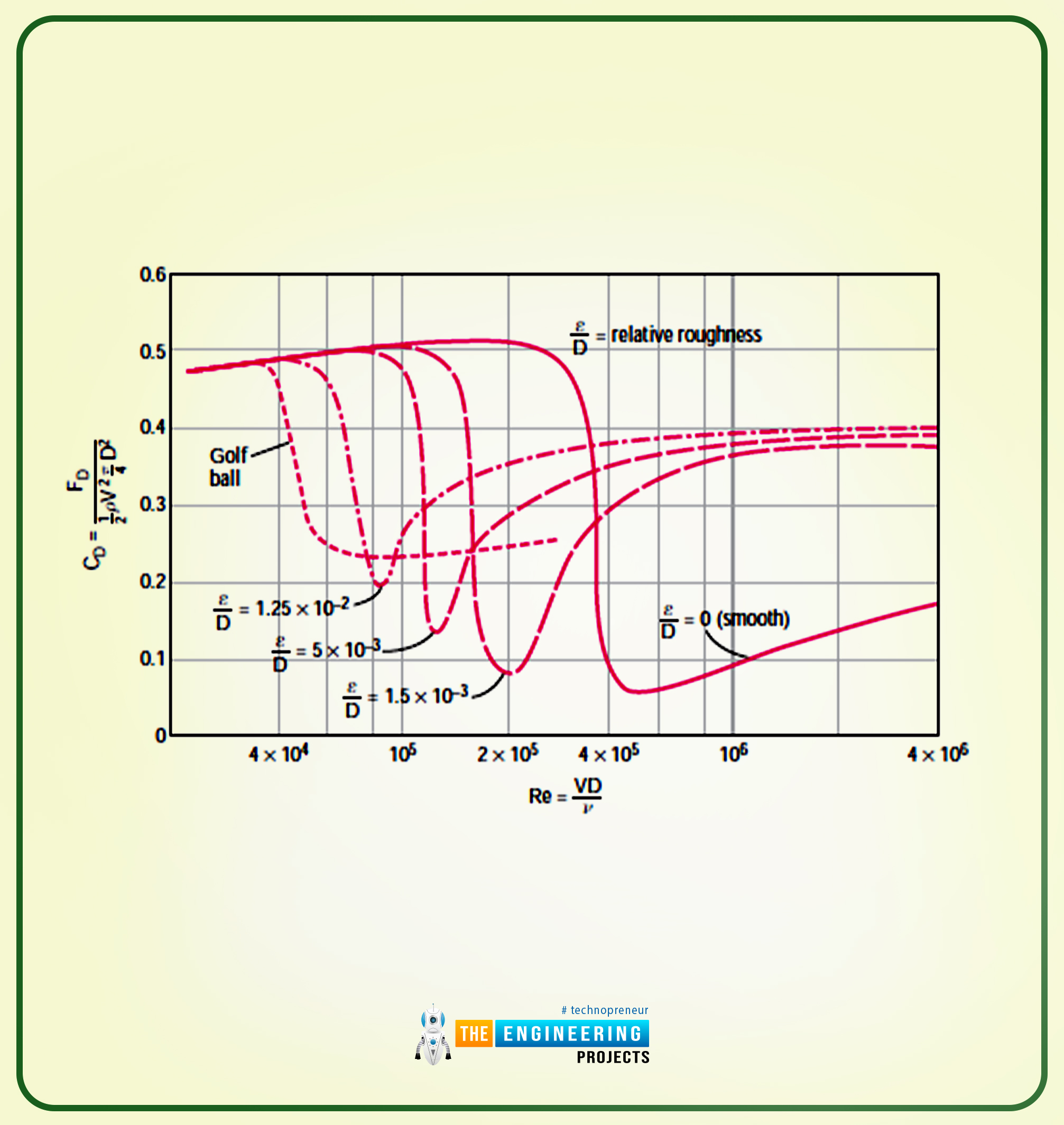
The oblique relation is finished by tripping the boundary layer into turbulence on the decrease worth of Reynold’s quantity. The result’s that the fluid is shut in behind the physique, decreasing the strain drag drive.
The worth of Reynold’s quantity is Re≅2×105, and the worth of the drag coefficient is CD≅0.1 within the case of a tough floor together with D=0.0015. Within the case of a easy floor, the values adjustments, they usually develop into CD≅0.5.
The worth of Reynold’s quantity for the tough sphere is Re≅106, and the drag coefficient worth is CD≅0.4.
So the worth of the drag coefficient for a easy sphere is CD≅0.1.
The rougher the sphere will develop into, the extra drag will even improve.
In an effort to exemplify the values, allow us to take an instance of a golf ball. The rate worth ranges from 15 to 150m/s for the golf ball, and the worth of Reynold’s quantity is 4×105,.
Raise
Firstly of the article, I’ve already mentioned what elevate is. Right here on this subject, I’ll clarify extensively concerning the elevate and the mathematical equation.
In an effort to clarify the subject in a symmetric method, I’ll clarify it in key factors, and these are as follows:
As you recognize that elevate is the part of the online drive, and this web drive is due to the viscous and strain drive.
The coefficient of the elevate is defined as follows:
CL=FL12V2A
The A right here presents the planform space, and this space is seen by somebody that’s taking a look at it from above in a course regular to the physique.
The V is the upstream velocity.
We’ll think about the airfoil with a width b and chord size c and the planform space as A=bc, respectively.
The next is the diagram that reveals the airfoil construction.
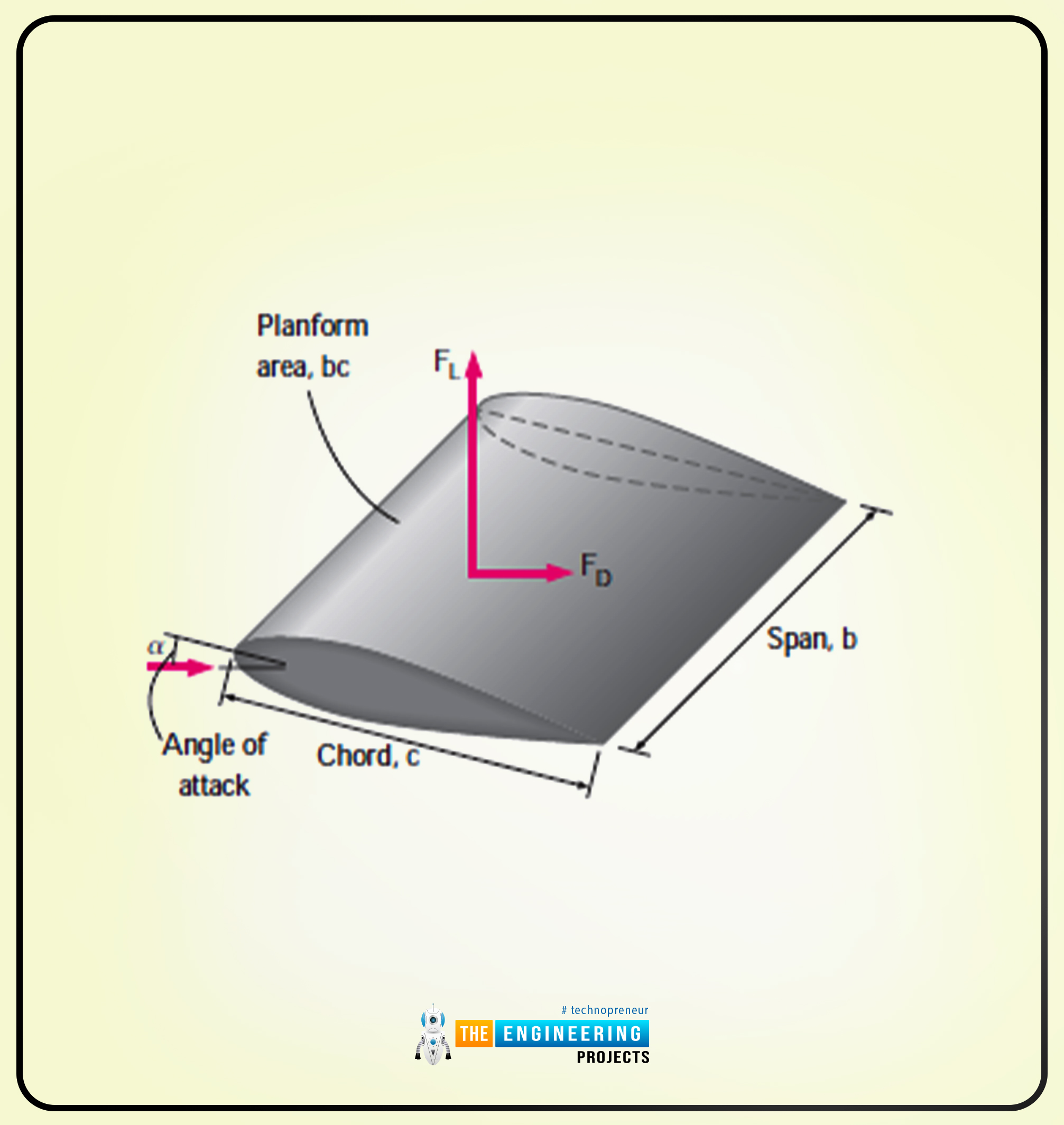
Right here, there’s a time period referred to as wingspan or span. It’s the distance between the 2 ends of the foil.
Within the case of plane, the wingspan is the full distance between the guidelines of two wings.
One other necessary time period is wing loading. It’s the common elevate per unit planform space FLA.
The airplanes are all based mostly on the elevate.
The aim of discussing the elevate intimately is to know the way airfoils are designed and the way they generate elevate by holding the worth of drag minimal.
The streamlined our bodies, resembling airfoils that intends to generate the elevate, have a negligible elevate, and the wall shear is parallel to the floor.
I’ll present you the pictorial illustration of the irrotational and precise move previous the non-symmetrical two-dimensional airfoils.
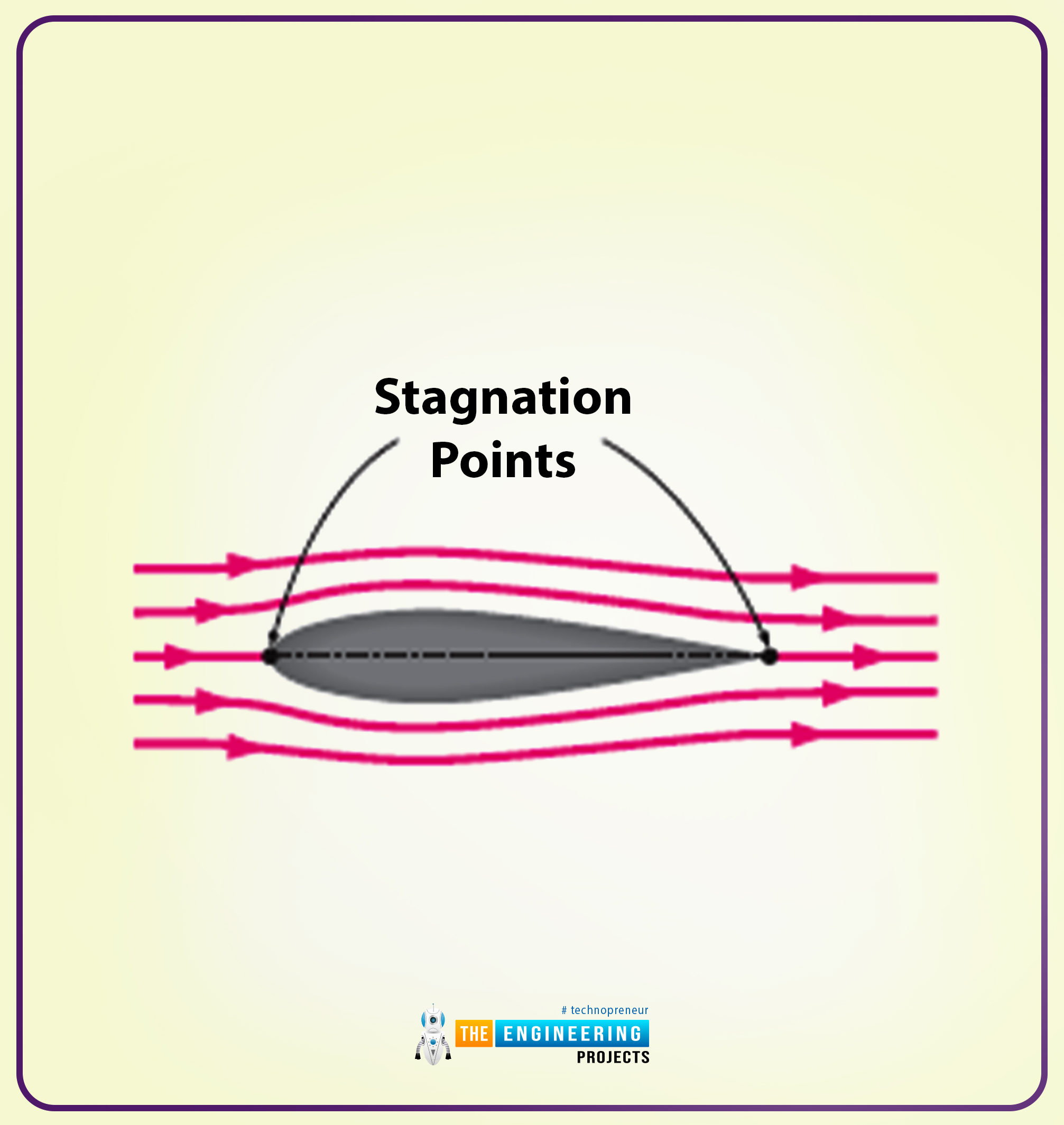
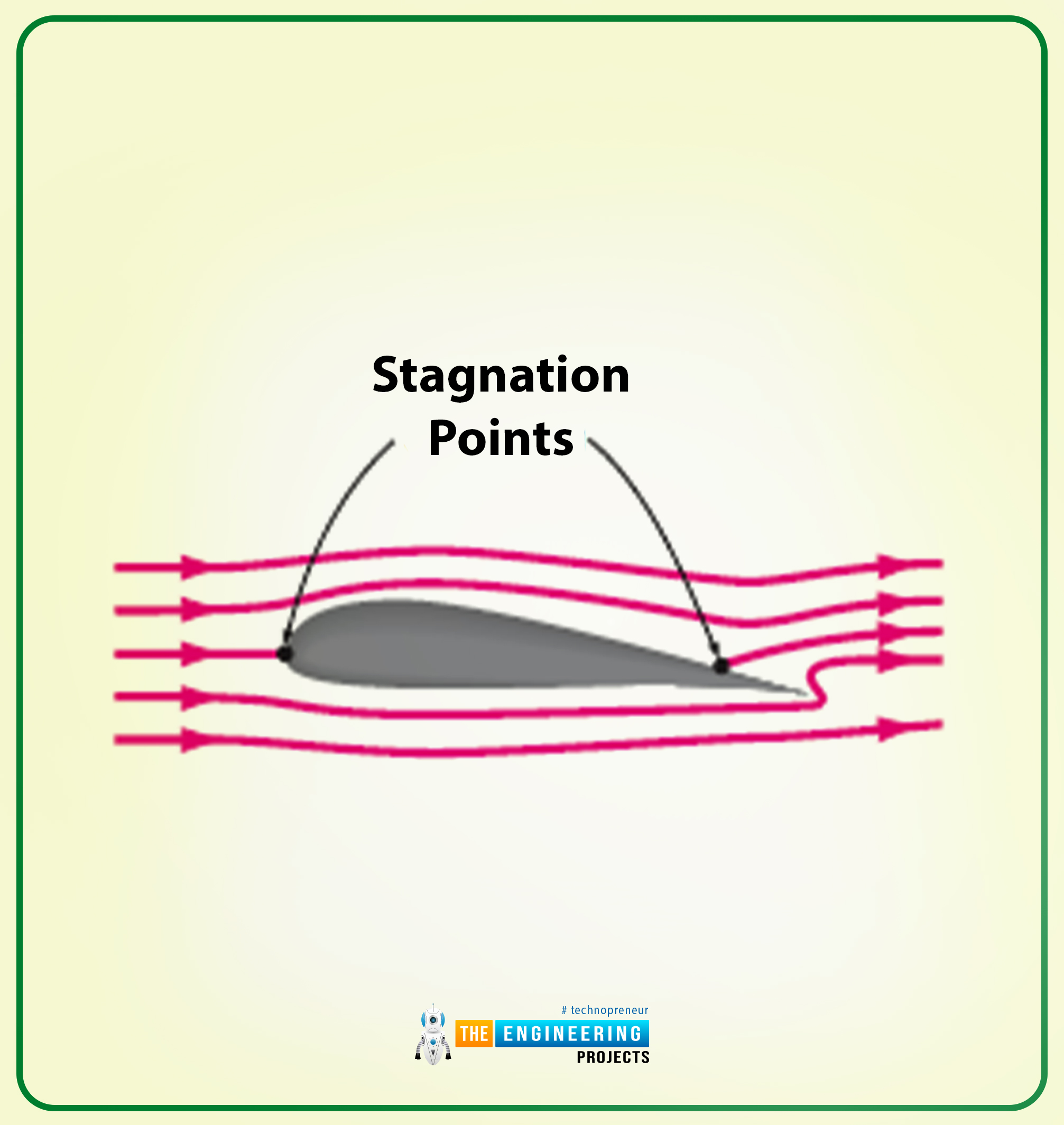
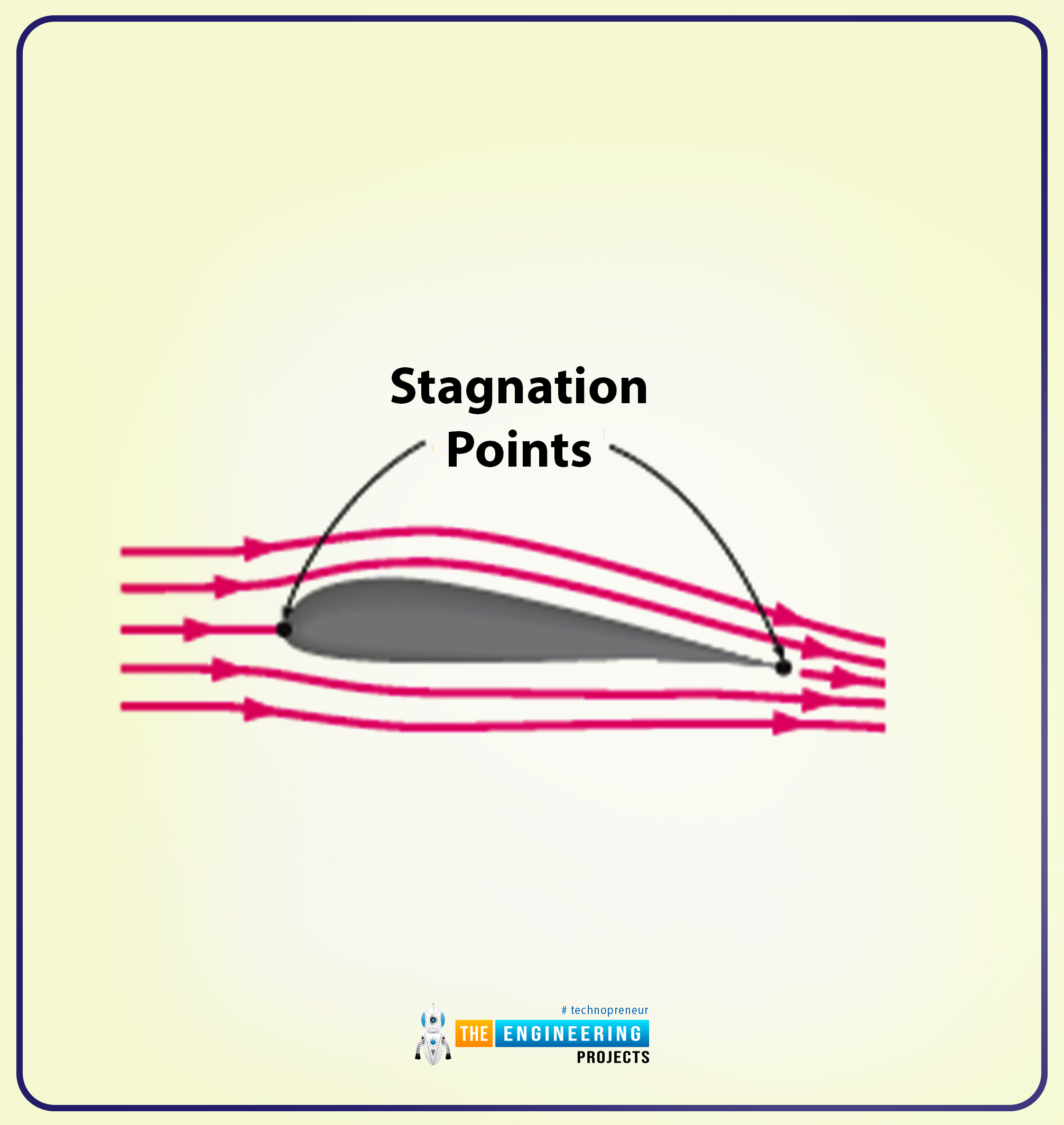
Conclusion
Hope you get pleasure from studying the article. I’ve tried my finest to elucidate you each level in simple phrases. Thanks for studying.


0 Comments