[ad_1]
Within the early 1800’s, a French Mathematician often known as Baron Jean Baptiste Joseph Fourier studied the conduction of warmth in numerous objects and got here up with a mathematical evaluation on the topic, which later grew to become the well-known Fourier Sequence. There are quite a few engineering issues within the fields of Communication, RADAR, Imaging, Audio, and many others. that includes the notion of Fourier Seres (and Fourier Transforms, which is a subject for another time). As an example, all energy indicators within the subject of communication have a detailed affiliation with Fourier Sequence whereas power indicators with Fourier Transforms.
However what precisely is the Fourier Sequence? What are Fourier Coefficients and methods to derive them? What are the functions of Fourier Sequence? We are going to discover out solutions to all these questions on this information.
Introduction
When Joseph Fourier launched his mathematical mannequin on conduction of warmth to the Academy of Sciences in Paris in 1807, they criticized and rejected his work. However later, when he printed this work in his ‘Théorie analytique de la Chaleur’ (or The Analytical Idea of Warmth) in 1822, it grew to become an integral a part of engineering.
Regardless that the unique mathematical evaluation was a examine of conduction of warmth in metals, engineers discovered that they may apply the identical method for different mathematical, engineering and physics issues.
At this time, you’ll be able to see Fourier Sequence is essential within the fields of Communication (RADAR, Satellite tv for pc, Wi-fi basically), Acoustics, Picture Processing (Sign Processing basically), Electrical, Optics and lots of extra.
What’s the Fourier Sequence?
Okay. Sufficient introduction. Allow us to now concentrate on the principle query: What’s the Fourier Sequence? Fourier Sequence is an Infinite Sequence of a periodic operate by way of Sine and Cosine features.
Fourier Sequence of a periodic waveform is an infinite sum sine and cosine waveforms, the place the frequency of every wave (sine and cosine) is an integral a number of of the periodic waveform’s elementary frequency.
With none mathematical evaluation, these statements may sound ridiculous: why are we turning a easy waveform into a fancy mixture of trigonometric features?
Truly, the ensuing Fourier Sequence simplifies the method of sign evaluation of the principle operate (or waveform) at totally different frequencies. We are able to derive Fourier Sequence for any periodic or steady features or features with discontinuous values and its derivatives.
Earlier than continuing additional, we have to perceive the fundamental terminology we talked about earlier: the Periodic Perform. A operate f(x) is periodic if for a continuing T>0, f(x + T) = f(x). Right here, T is called the Interval of the operate.
Periodic Perform: f(x + T) = f(x), T>0
f(x) = f(x +2T) = f(x + 3T) = … T is the interval of the operate f(x). The operate f(x) repeats itself after equal intervals. Trigonometric features reminiscent of sin(x), cos(x), tan(x) and many others. are some easy examples of periodic features.
Now, coming again to the Fourier Sequence, if f(x) is a periodic operate, then we will categorical it as an infinite sum of sine and cosine features as follows:
Right here, a0, an and bn are often known as Fourier Coefficients. The values of those coefficients are what outline the Fourier Sequence of a operate. Fixed a0 is the typical worth of the periodic operate whereas an and bn are the amplitudes of assorted sinusoidal features.
We are able to calculate a0, an and bn utilizing the next expressions. For instance, if f(x) is a periodic operate, then Fourier Coefficients of its Fourier Sequence within the interval T ≤ x ≤ T+2π are as follows:
The equations of a0, an and bn are often known as Euler’s Formulae.
Within the earlier Fourier Sequence equation, we used each sine and cosine features. However we will additional modify the equation to present an equation solely by way of sinusoids.
We’ve the time period ancos(nx) + bnsin(nx) within the equation. We are able to re-write this as follows:
Utilizing these phrases, we will derive the sinusoid solely Fourier Sequence Expression of a operate as:
Within the above equation, discover that for n = 1, the sinusoidal amount has the identical frequency as the principle operate (which is ‘x’ on this case) and it’s the Basic Frequency of the principle waveform. All the next frequencies (for n = 2, n = 3 and so forth) are integral multiples of this elementary frequency which we name as Harmonic Frequencies.
So, for n = 2, the frequency of the corresponding sinusoid is called Second Harmonic. Equally, for n = 3, it’s Third Harmonic and many others.
Derivation of Fourier Coefficients
From the above dialogue, it’s clear that the Fourier Coefficients a0, an and bn are the crucial values that we have to calculate for any Fourier Sequence. We’ve already seen the expressions for these constants however allow us to attempt to derive them.
For this, allow us to assume that f(x) is a periodic operate and its Fourier Sequence for the interval [T, T+2π] i.e., T ≤ x ≤ T+2π is given by:
Expression for a0
Within the above equation, allow us to combine either side from x=T to x=T+2π. We get:
From the above equation, we will get the expression for a0 as:
Expression for an
Now, contemplate the unique Fourier Sequence expression as soon as once more. Multiply either side by ‘cos(mx)’ and combine the ensuing equation from x=T to x=T+2π.
Within the above expression, should you observe carefully, the integrals comparable to a0 and bn (first and third) are at all times zero. Coming to the second integral comparable to an, for all m ≠ n circumstances, it turns into zero and the one potential end result is for worth m = n. Due to this fact,
From the above equation, we will get the expression for an as:
Expression for bn
Now, contemplate the unique Sequence expression as soon as once more. Multiply either side by ‘sin(mx)’ and combine the ensuing equation from x=T to x=T+2π.
Within the above expression, the integrals comparable to a0 and an (first and second) are at all times zero. Coming to the third integral comparable to bn, for all m ≠ n circumstances, it turns into zero and the one potential end result is for worth m = n. Due to this fact,
From the above equation, we will get the expression for bn as:
Tips on how to Get hold of Fourier Sequence of a Perform f(x)?
Peter Gustav Lejeune Dirichlet formulated adequate situations {that a} periodic operate should fulfill with a view to derive Fourier Sequence. These are popularly often known as ‘Dirichlet’s Situations’.
We are able to categorical any operate f(x) in its Fourier Sequence type as:
The place a0, an and bn are constants if the next “adequate situations” are glad.
- The operate f(x) is a periodic, single-valued, well-defined and finite operate.
- It has a finite variety of discontinuities in any interval.
- f(x) has finite variety of maxima and minima in a bounded interval.
If these situations are met, then we will acquire the Fourier Sequence of any operate utilizing the next steps:
Assume the generic type of Sequence with respect to the operate as follows:
Calculate the worth of a0 utilizing the next components:
Compute the worth of an utilizing the next expression:
Calculate the worth of bn utilizing the next components:
Now, substitute the values of a0, an and bn within the authentic expression (from Step 1) and you’ve got the ultimate Fourier Sequence of the operate f(x).
Fourier Sequence Purposes
The idea of representing any waveform (or operate) purely by way of sinusoids is a strong instrument in arithmetic, engineering (electronics, communication, mechanical, and many others.), acoustics, picture and video processing.
Fourier Sequence and Fourier Transforms, which collectively type a brand new set of mathematical modelling often known as Fourier Evaluation, are essential in a number of scientific functions to resolve bizarre and partial differential equations, sign processing, statistics, seismography, oceanography, sonar, cryptography and many others.
Conclusion
This was an introductory information on Fourier Sequence. Joseph Fourier developed a mathematical mannequin of conduction of warmth in metals, which later grew to become the Fourier Sequence. On this, we will signify any steady, periodic operate (waveform) purely within the type of sinusoids. We’ve seen the fundamental Fourier Sequence expression, Fourier Coefficients, Dirichlet’s Situations and lots of extra.
[ad_2]


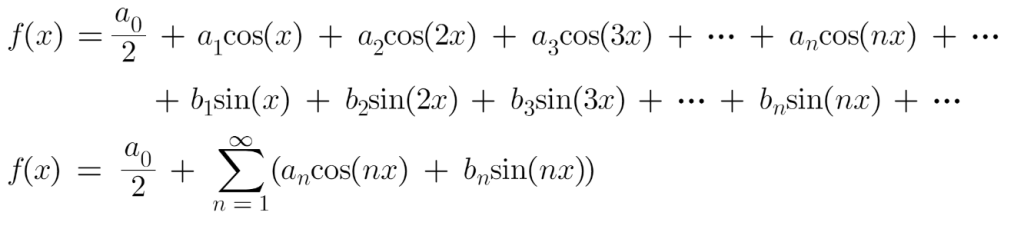
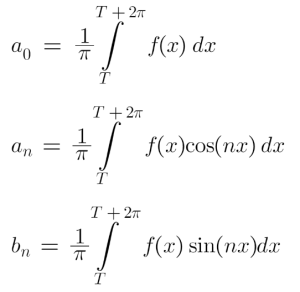
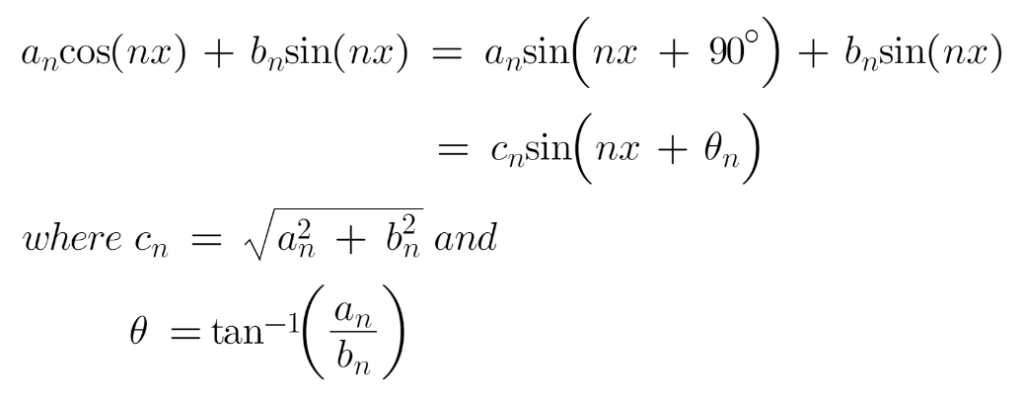
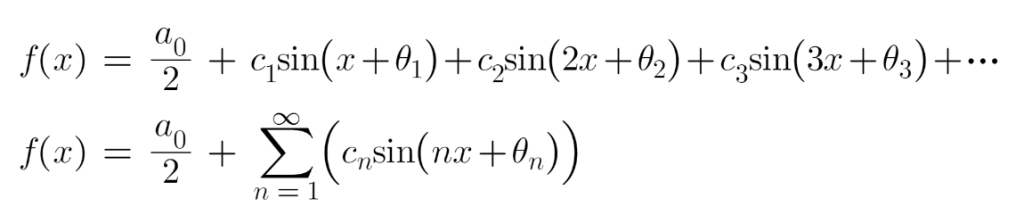

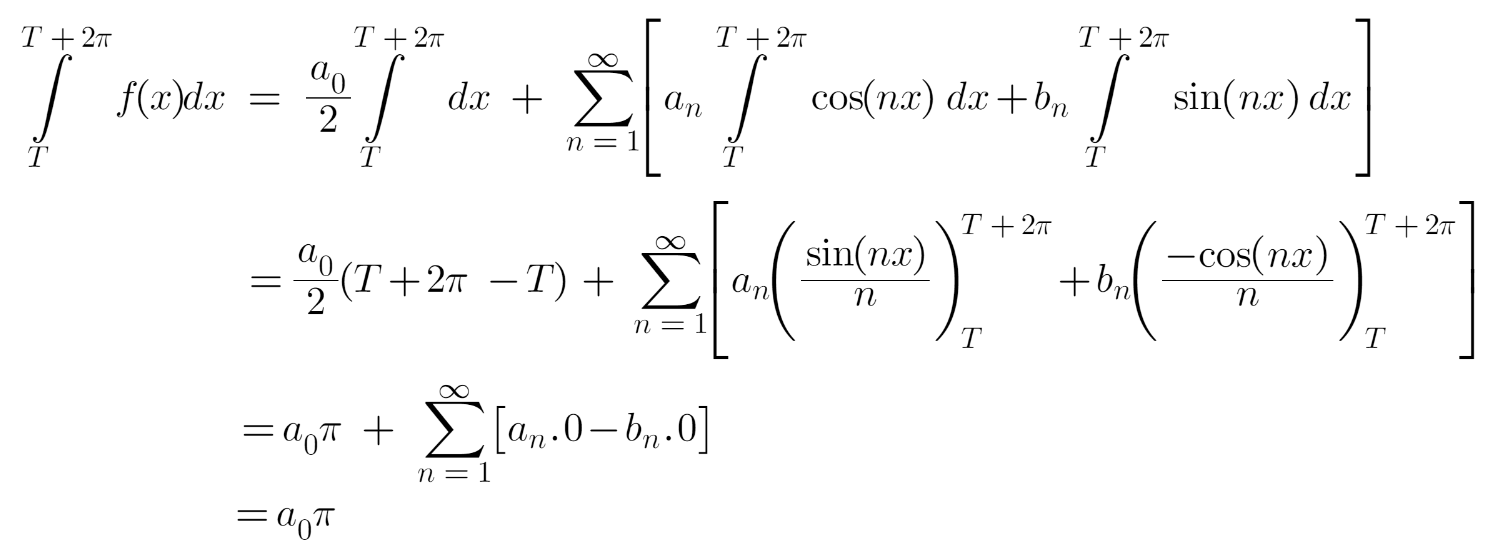
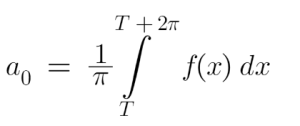
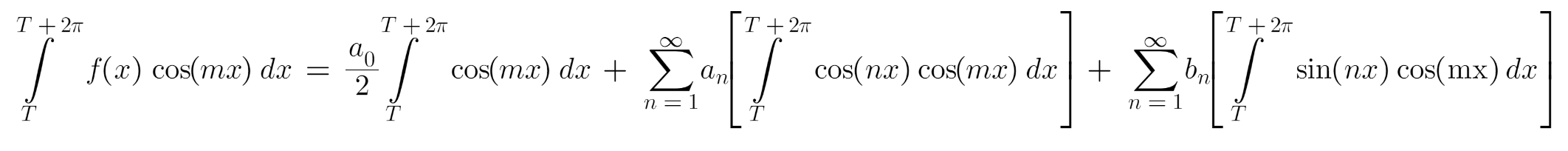
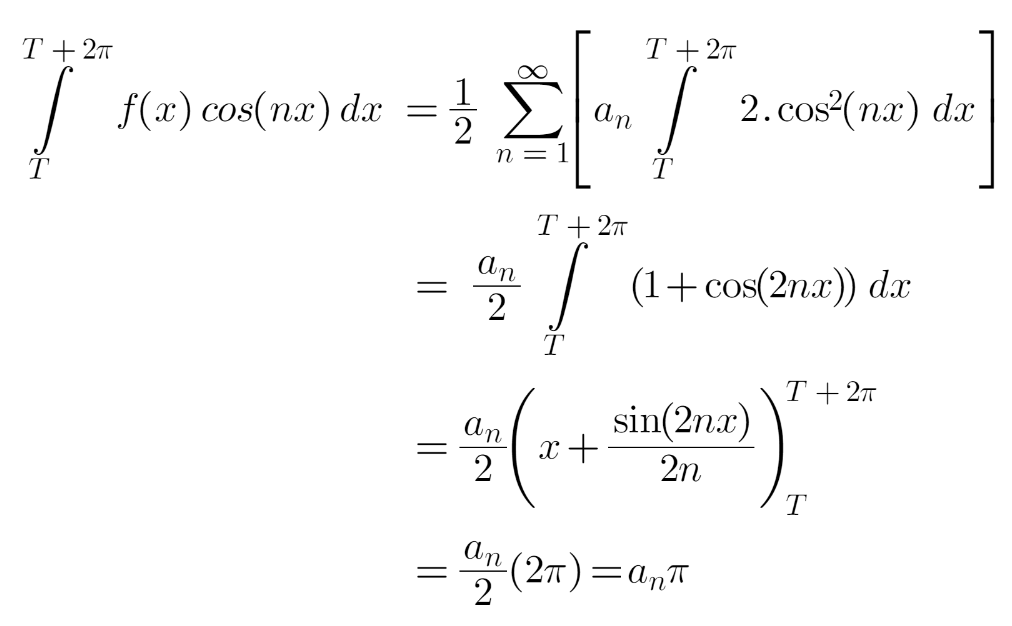
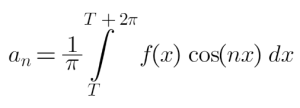
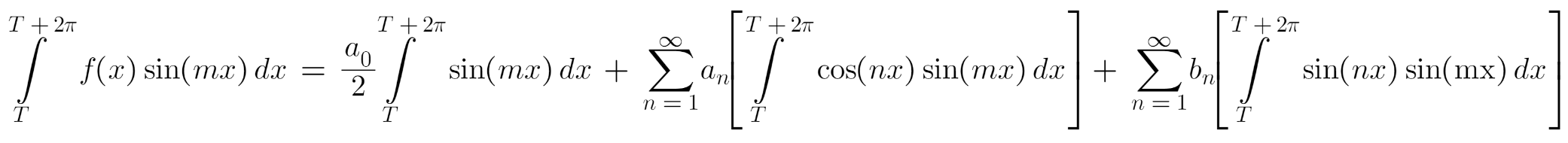
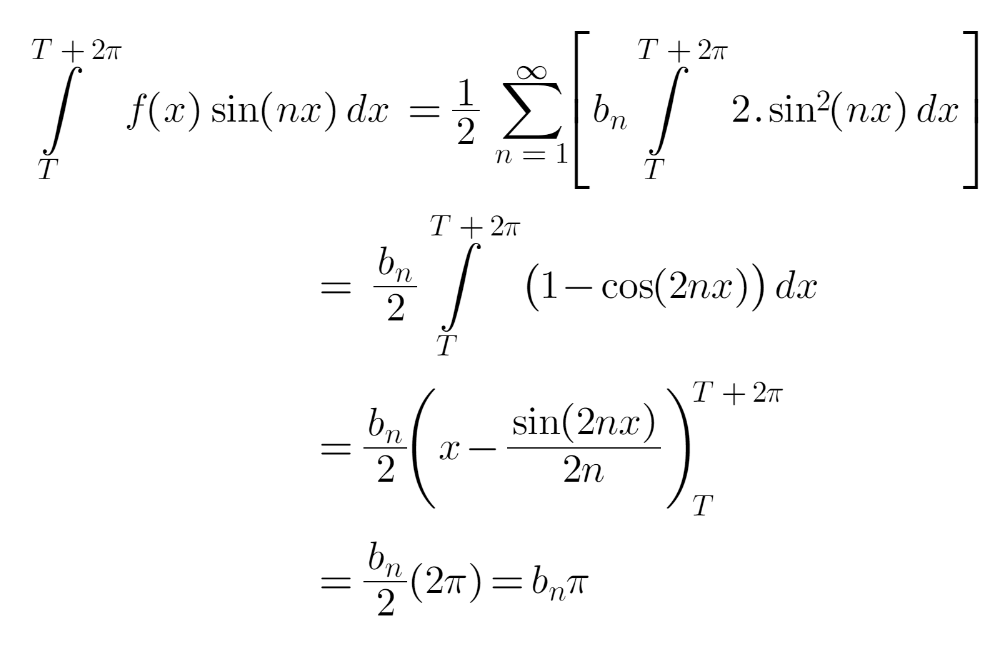
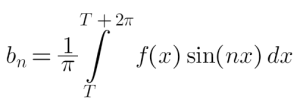


0 Comments